Interest rate neutrality is easy to state in equations but hard to digest intuitively.
The equation says that interest rate = real rate plus expected inflation, \[i_t = r + E_t\pi_{t+1.}\]In one direction this is easy: If people expect a lot of inflation, then they demand higher nominal \(i_t\) interest rates to compensate for the declining value of the dollar. That leaves the real \(r\) interest rate unchanged.
(Note: this post uses mathjax equations. If you can't see them, come to the original.)
But in our economy the Fed sets the nominal interest rate and the rest must adjust. In the short run with sticky prices and other frictions the real rate may change, but eventually the real rate is set by real things and expected inflation must rise. We can study that long run by leaving out the sticky prices and other frictions, and then expected inflation rises right away. Rises. Higher interest rates raise inflation. How does that really work? What's the economic force?
Standard intuition says overwhelmingly that higher interest rates cause people to spend less which lowers inflation. The equations seem like they're hiding some sort of sophistry.
(Fed Chair Powell explains the standard view well while sparring with Senator Warren here. The clip is great on several dimensions. No, the Fed cannot increase supply. No, none of what Senator Warren talks of will make a dent in supply either. The elephant in the room, massive fiscal stimulus, is not mentioned by either party. Just why each is silent on that is an interesting question.)
This is a lovely case that individual causality goes in the opposite direction of equilibrium causality. That happens a lot in macroeconomics and can cause a lot of confusion. It also is an interesting case of mistaking expected inflation for unexpected inflation. Along with confusing relative prices for inflation, that's common and easy to do. Hence this post.
Start with the consumer first order condition, or "IS curve" of new-Keynesian models, \[ x_t = E_t x_{t+1} - \sigma (i_t - E_t \pi_{t+1}-r) \] with \(x=\) consumption, output or output gap after linearization, \(i=\) nominal interest rate, \(\pi=\) inflation and \(r\) equal the discount rate or long-term real interest rate. To the individual, the interest rate and expected inflation -- the price levels \(p_t\) and \(p_{t+1}\) and thus \(\pi_{t+1}=p_{t+1}-p_t\) -- are given, exogenous. (Minus not divided by, these are all in logs.) The consumer chooses consumption \(x\) subject to a budget constraint. If the Fed raises interest rates and prices do not yet adjust, then the consumer wishes to lower consumption today \(x_t\) and raise consumption tomorrow \(x_{t+1}\). That is the standard intuition, and correct.
Now, a desire to lower consumption today pushes down the price level today, and consuming more tomorrow pushes up the price level tomorrow. More deeply, let's pair this first order condition with equilibrium in an endowment economy, with constant \(x_t=x\). In English, fix supply -- there is only so much output \(x\) to go around so prices have to adjust until people are content to buy what's on the shelves, no more and no less. (We can also pair it with the Phillips curve, and then specify flexible prices.) The current price level \(p_t\) falls relative to the expected future price level \(p_{t+1}\) until the consumer's demand equals supply, so \( E_t\pi_{t+1} = i_t+r\). Expected inflation rises to meet the interest rate. As promised, and by exactly the conventional mechanism.
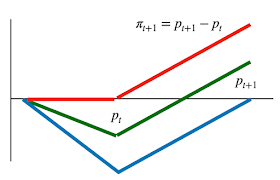
This logic tells us that the higher interest rate produces higher future inflation, from this year to next year. Now, you can get higher inflation by a lower initial price \(p_t\) or from a higher later price \(p_{t+1}\). The graph below shows the two possibilities, and (green) an intermediate possibility.
So the original intuition can be right: Higher interest rates might well depress current demand and lower \(p_t\). (Blue line) That produces lower ex post inflation \( \pi_t=p_t-p_{t-1}\) and higher expected inflation \(E_t\pi_{t+1}=E_t(p_{t+1}-p_t)\). The intervention can well "lower inflation," in this sense. This is how standard (new-Keynesian) models work.
If we stop here, the confusion is just semantic. As often in life, you can resolve a lot of seemingly intractable arguments just by defining terms more carefully. Higher interest rates can lower current inflation. Sticky prices and other frictions can draw out this period of decline. As for the price recovery, and higher future inflation, well, we often do see that -- inflation comes back as it did in the 1970s -- or maybe the Fed doesn't leave interest rates alone long enough to see it. The long run is a long time.
But there is another possibility. Maybe the higher expected inflation all comes from a higher future price level, not a lower current price level; the red line not the blue line. Which is it-- higher \(p_{t+1}\) or lower \(p_t\)? This first order condition is not enough to answer this question. You need either new-Keynesian equilibrium selection policies or fiscal theory to determine which one it is. In either case, it comes down to fiscal policy. To have an unexpected decline in inflation, Congress must raise tax revenue or cut spending to pay off bondholders in more valuable money. If Congress refuses, we get the top line, more future inflation, no inflation reduction today. If Congress goes along, we can get the bottom line. Fiscal and monetary policies always work in tandem.
But this post is about the narrow question: Why do higher interest rates raise expected future inflation? If it happens by lowering the current price level, producing an unexpected deflation, that's consistent with the question. So part of the intuitive problem was understanding the question, and in the verbal debate one side (conventional, implicitly) was talking about unexpected current inflation, while the other (Fisherian) side was talking about expected future inflation. Both can be right!
To the individual, the price levels and expected inflation are exogenous and the consumption \(x\) decision is endogenous. In equilibrium, the endowment \(x\) is exogenous, and the price levels and expected inflation follow. This is the same clever reversal of the famous Lucas asset pricing model. The individual chooses consumption seeing asset prices. In equilibrium, changes in the endowment cause changes in asset prices.
(Thanks to the colleagues who pressed me to find a good intuition for this result.)
The Correct equation is: budget_deficit_rate = long_run_inflation = long_run_risk_free_interest_rate, b = i = r.
ReplyDeleteThe mistake in the model is assuming that the interest rate is exogenous. In reality, it is the budget deficit that leads the way.
A positive government budget defict rate (deficit/money_supply) means that everyone expects inflation in the long run (ignoring real GDP growth as a function of tech for now).
The interest rate is merely a function of timing that inflation. If we want it now, then we'll just have the Fed lend to the Gov't. If we want the inflation later, the Fed tries to offset the budget deficit by not lending everything the Government needs. When that happens, private investors take cash out of the economy and invest it in government bonds.
Just to illustrate, if the entire budget deficit were covered by private investors, there would be no net increase to the quantitiy of money available in the economy. There would be no inflattion....for the moment.
The problem, is that eventually that debt will have to be paid back with interest. Unless the Government can collect the interest payments as well from private individuals via taxes, they will have to increase the money supply eventually.
Thus, the correct equation is: budget_deficit_rate = long_run_inflation = long_run_risk_free_interest_rate, b = i = r. We can also figure that the long_run real GDP growth rate, as a function of permanent technology shocks, is going to be some equilibrium. Similarly, the long-run riskiness of the economy and time-preference is a constant.
Assume that in the long run, rates of b,i,and r will all gravitate toward each other. Occasionally, there will be shocks that will cause one to divert, but in the long-run, they are all going to be equal.
We then have: change in inflation rate = 0.5*change in budget deficit rate + 0.5*change in interest rate. Or Change in interest rate = 0.5*change in in deficit rate + 0.5 change in inflation rate.
Presumes that government must sell bonds (borrow) to finance deficits - they don't.
DeletePresumes that interest is strictly the cost of borrowing - it isn't.
This comment has been removed by the author.
ReplyDelete"This is a lovely case that individual causality goes in the opposite direction of equilibrium causality. That happens a lot in macroeconomics and can cause a lot of confusion." Reminds me of my favorite Milton Friedman clip: https://youtu.be/8hlpDxdbj5w?t=1545
ReplyDeleteGreat Friedman clip.
DeleteI am James Cover at profcover@gmail.com. I think you need an equation that represents or helps determine what future policy is going to be. For example in your model how much demand changes will depend on whether the monetary authority is targeting inflation or targeting the price level and you cannot really get an Ep(t+1) without knowing what the nominal rate of interest will be next period. So I think trying to think about this in too simple a model can be misleading. Anyway, my colleague Paul Pecorino and I show in a SEJ paper from many many years ago in a model that adds a couple of simple equations that the variance of output is lower if the Fed targets the price level rather than inflation.
ReplyDeleteJust a small quibble…. “ But in our economy the Fed sets the nominal interest rate and the rest must adjust.” Could it be that the FED funds rate just follows and doesn’t lead market determined rates?
ReplyDeleteI used to believe that too, until the data unequivocally taught me otherwise. See here
Deletehttps://www.johnhcochrane.com/research-all/the-fed-and-interest-rates-a-high-frequency-identification
The post is a theoretical question, however. IF the Fed pegs the nominal interest rate--which it can, even if you don't think it did--then how does expected inflation rise?
"Could it be that the FED funds rate just follows and doesn’t lead market determined rates?"
DeleteI think it would depend a lot on this:
https://fred.stlouisfed.org/series/FDHBFRBN
And this:
https://data.nasdaq.com/data/USTREASURY/AVMAT-average-maturity-of-total-outstanding-treasury-marketable-securities
What does a "market determined rate" even mean when the FOMC is the largest single owner of federal debt? ($6 Trillion of a little over $30 Trillion = 20%)?
Which inflation rate? Which interest rate?
DeleteJohn, if higher interest rates predict higher future consumption and inflation, wouldn't rational agents adjust prices immediately and inflation would actually arise today with the increase of nominal rates? The red line wouldn't be flat at p_t, but upward sloping instead. Is that a possibility?
ReplyDeleteIn the paragraph in which the first sentence begins with "Now, a desire to lower consumption today pushes down..." there appears to be an error concerning the relation between the rate of interest in the current period, i(t), and the conditional expectation of the next period rate of inflation E_t{\pi_(t+1)} under the fixed periodic income endowment, x(t) = x. With x(t) pinned down at level x, the conditional expectation of x(t+1) formed in period t, i.e., E_t{x_(t+1)}, must of necessity be equal to x also. This constraint then requires that ( i(t) - E_t{\pi_(t+1)} -r ) = 0 for \sigma > 0. The only condition under which i(t) = E_t{\pi_(t+1)} is when r = 0 which would represent a special situation and not one generally prevailing in New Keynesian models in the literature. If r = 0, then the representative consumer's cost function would be unbounded.
ReplyDeleteInstead of i(t) = E_t{\pi_(t+1)} determining the pathwise development of expected inflation, the pathwise development would be determined by the relation \delta E_t{\pi_(t+1)} = \delta i(t). Which is to say that the increment of change in the rate of nominal interest is matched by an increment of change in the expected future period inflation rate, one-for-one. This is consistent with the constraint x(t) = x and the corresponding derived requirement ( i(t) - E_t{\pi_(t+1)} -r ) = 0 .
In part, you note a typo now fixed: i_t = E_t \pi_{t+1} + r, and the +r was missing. In part though, the logic is off. x_t = x is an equilibrium condition for the aggregate economy, not a budget constraint for the individual. Facing prices, people do think they can lower x today and raise it tomorrow. Prices adjust until they are happy choosing to consume what's available.
DeleteIn defence of my contention above, I note that the development of the Euler equation on which the new-Keynesian IS Curve is predicated is based on the assumption of a representative household's cost function, i.e., ∑ βᵗ U(cₜ). The log-linear approximation, given by the new-Keynesian IS Curve is predicated on the assumption that cₜ = yₜ and xₜ = ln(yₜ) – ln(yₜ⁺), where yₜ = current gross domestic product, and yₜ⁺ = current potential gross domestic product; xₜ = output gap in the current period, t. If xₜ is pinned down by specifying xₜ = x, then Eₜ{xₜ₊₁} is pinned down also, i.e., Eₜ{xₜ₊₁} = x , under the rational expectations hypothesis. The assertions in my earlier remarks then follow from the assumption of an infinite-lived representative household decision-maker who optimizes the present value of life-time consumption (expressed as the rep. hshld's cost function, above).
DeleteIf we are to assume that the representative household is not representative of all households in the model economy, then we must find another expression for the new-Keynesian IS Curve that fits that specification. For example, an overlapping-generations model, or a model in which some households can save, but others cannot for want of sufficient income. Then, we must provide a rationale for the impact of some households deferring consumption, while other households do not, on the price level in the current and future periods. Is the price level responsive to the fraction of households deferring relative the households who do not? What is the critical fraction threshold? &c. These observations pertain to the "endowment economy" in which the first-order necessary condition for an optimal policy maximizing the present value of the utility of consumption of the rep. hshld. (the Euler eqn.) applies. Relaxing the "endowment economy" constraint imposed on the n-K IS Curve log-linear approximation negates the complementary constraint σ∙( iₜ – Eₜ{πₜ₊₁} – r ) = 0.
My remarks do not impugn your conclusion: "This logic tells us that the higher interest rate produces higher future inflation", though I would condition the conclusion by adding "expectations of" between "produces" and "higher" to be consistent with the revised last sentence of the paragraph preceding your conclusion.
Aside: I have prepared further remarks supporting the thrust of this article based on quotations from Jean-Baptiste Say (1834) and the Foley, et al., (1969) article in the J. Pol. Econ. referred to in an earlier remark (comment) made on another article in this thread, but I will hold off posting for the time being.
A speech and then a paper from the Bank of Canada discussing bank policy in the face of supply disruptions and the resulting inflation that might be relevant to the discussion of interest rate policy and inflation expectations.
ReplyDelete(1) A speech transcription, "Macroeconomics of the 2020s: What we’ve learned, and what’s to come", Remarks by Paul Beaudry, Deputy Governor, to the University of Waterloo Faculty of Arts, Distinguished Lecture in Economics, September 20, 2022, Waterloo, Ontario, Canda. 11 pp. https://www.bankofcanada.ca/wp-content/uploads/2022/09/remarks200922.pdf
(2) A working paper, "Looking Through Supply Shocks versus Controlling Inflation Expectations: Understanding the Central Bank Dilemma", by Paul Beaudry, Thomas J. Carter, and Amartya Lahiri. Ottawa. Bank of Canada: Staff Working Paper/Document de travail du personnel—2022-41. 51 pp. Last updated: September 20, 2022. https://www.bankofcanada.ca/wp-content/uploads/2022/09/swp2022-41.pdf
The speech is interesting for its discussion of the differences between central bank policy responses in 1979-1982, 2001, 2007-9, 2020-22. Charts in the transcription illustrate the differences in macro-economic recovery rates and the forces bearing on those recoveries that limited or promoted inflationary episodes.
The working paper presents a theoretical model focusing on supply-side disruptions and central policy options. The model addresses 'adaptive expectations' and 'rational expectations' and the shortcomings of each, and suggests a 'k-level' expectations approach. The standard new Keynesian IS curve is presented in sub-section 2.5, and expectations models are discussed in Section 3. The mathematics is tractable, but dense. Proofs of the propositions are found in the appendices. An analytical solution is presented for a few special cases; otherwise, numerical computer solutions are required to reach 'optimal' solutions to the n-households infinitely-lived optimization problem. The households' cost function is a conventional log-utility function on consumption coupled with a linear penalty for labor hours worked, i.e., U(cₜ , Nₜ ) = ln(cₜ) - η∙Nₜ . As is always the case, the choice of cost function and state equations always limits the generality of the optimization problem. Nonetheless, the paper is of interest as an application of a modified 'rational expectations' model that may be closer to the real world behavior than a purely 'rational expectations' model can attain.