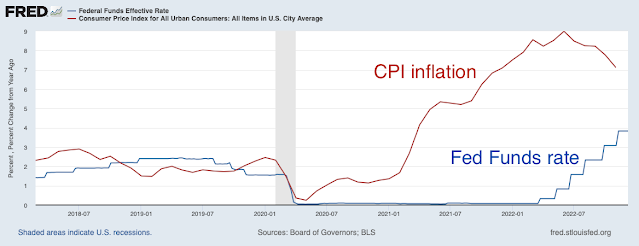
The November CPI is in, and inflation continues to moderate despite interest rates that, while rising, are still below current inflation. The great experiment seems to be working out, at least for now. (Previous post, with links to earlier writing.)
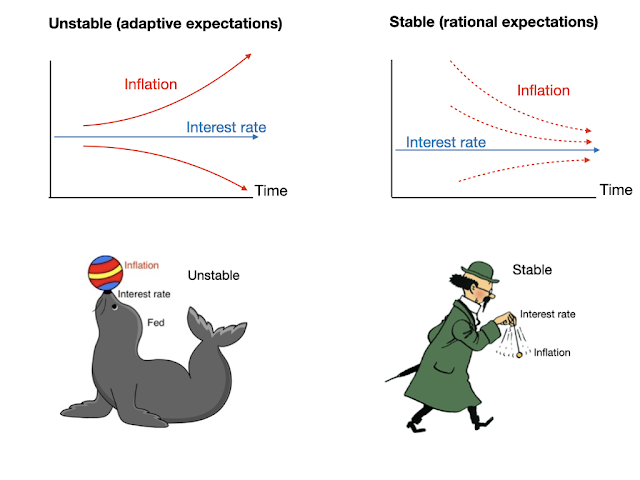
As before, the first great question, which economists really don't have a consensus answer to, is whether inflation is stable or unstable; whether it takes a period of interest rates above current inflation to bring inflation down, or whether inflation will eventually follow the interest rate.
(Yes, I've used this picture several times before, but it's too much fun not to use again.) In the conventional "adaptive expectations" view, inflation is unstable, like the ball on the seal's nose, unless the Fed moves interest rates quickly, and inflation will spiral away unless interest rates rise above the current rate of inflation. In the more radical "rational expectations" view, inflation is stable and will eventually go away on its own even if the Fed does nothing. (So long as fiscal policy doesn't add fuel to the fire. Also, it allows for more dynamics; inflation can go up before coming back, and the long run can take a long time.)
The experiment, like the zero bound era, seems to be coming in on the side of stable.
What about the Fed's rise in rates? In the models I play with, that will help in the short run, but at the cost of stubborn more entrenched inflation eventually. To recap, here is the response of a simple fiscal theory model to a fiscal shock -- deficits that people do not expect to be repaid -- when the Fed does nothing (top), and to a monetary policy shock -- persistently higher interest rates with no change in fiscal policy -- (bottom).
In response to the fiscal shock, we get a drawn out period of inflation. The negative real interest rate (interest rate below inflation) slowly eats away at bondholder's wealth until they have, in essence, paid for the initial deficit. In response to higher interest rates, with no change in fiscal policy, inflation initially declines, but then eventually follows the interest rate. Remember, it's a "stable" model, meaning it has that "long run neutrality" in it, as a result of rational expectations.
These are the paths of inflation and interest rates after a one-time shock. As you interpret history, remember that every day is a new shock, and more shocks will come. Also the models are incredibly simplified, and obvious modifications add more realistic dynamics.
Ok, enough review. On the basis of the top graph, I thought inflation might well decline on its own, with interest rates staying below inflation, at least as long as we don't have another big fiscal blowout.
But now, the Fed is starting to respond (the novelty of today's post). How does that change things? Well, add the bottom graph to the top graph, really. As the Fed responds to inflation, that brings down current inflation -- a good thing -- but raises future inflation. With no change in fiscal policy, the Fed can rearrange inflation over time, but it can't get rid of the inflation that must eat away at the debt. It faces "unpleasant arithmetic" in Sargent and Wallace's famous view, though this is "unpleasant interest rate arithmetic" rather than "unpleasant monetarist arithmetic."
Another way to put it is that the Fed is starting to follow a Taylor rule, reacting to inflation by raising interest rates.
So, what happens? In these incredibly simplistic models, I simulated the response to a fiscal shock when the Fed does respond by raising interest rates, effectively automatically adding the bottom graph to the top graph. Here you go:
The solid inflation and output lines, and the lower solid interest rate line, repeat the top panel of the previous graph -- the effect of a fiscal policy shock if the Fed does nothing. The "with policy rule" lines with markers show what happens after a fiscal shock if the Fed instead follows a Taylor-type rule, interest rate = 0.9 times inflation. As you see in the blue line with markers, the interest rate now rises, in response to inflation, as the Fed is now doing. The result of that interest rate rise, per lower previous graph, is to bring down current inflation, at the cost of making inflation more persistent.
In the New-Keynesian model underlying all of this, the Fed's reaction is a good thing, even though it does not eliminate inflation. By lowering inflation, it reduces the effect of inflation on output via the Phillips curve. In this Phillips curve, inflation = expected future inflation + k x output gap, so a random-walk inflation is the best thing for stabilizing output. A Taylor rule with a 1.0 coefficient would do that. In adaptive expectations models, the Taylor rule brings stability. In new-Keynesian rational expectations models, it brings determinacy. In this fiscal theory new-Keynesian model, it reduces output and inflation volatility. The answer is the same, the questions change (rather drastically). That model robustness is a good thing, not an insult.
So, roughly speaking, here we are. Yes, my simulation supposes that the Fed reacts instantly, where it has taken a while. And reality has had multiple "shocks." So squint a bit. The lesson I see is that by adding higher interest rates a bit later in the game, the Fed is bringing inflation down (second graph) not just blunting inflation is it would have done had it moved earlier. But without progress on fiscal policy (a negative of the top graph), inflation will only subside to something like 4%, and then stick there rather stubbornly -- the right hand side of the last graph is the cost of blunting inflation now.
The episode is not totally an "experiment," as this seems to be the same forecast that others arrive at by other means. "Team transitory" thinks we had supply shocks that are fading, so inflation can go away without big interest-rate increases, but slow-moving expectations have risen. That view is not totally consistent, as with adaptive expectations, the period of no interest rate movement should have led to additional pressure on inflation. As they (or their intellectual ancestors) did in the 1980s, they think the Phillips curve pain of reductions will be too large, and are arguing that we should just get used to it and raise the inflation target. The option of a painless disinflation by fixing the long-run fiscal problem isn't in that worldview. But in any case, we get to roughly the same path going forward.

1975 may be a good historical precedent to think about. The Fed acted more quickly that it is doing now, but still never raised interest rates substantially above inflation as it did in 1980-1982. Nonetheless, inflation did fade. But it never got all the way back to its previous value, and then took off again with additional shocks in the late 1970s.



The chart where you add the first two together is a little busy (the black hashed lines and the lack of a legend make it difficult to follow, you also reference solid output lines that I don't see). It might be better to remove the black lines and just add hashed colored lines for with policy to the original one (keep it exactly the same otherwise, so keep the markers for it).
ReplyDeleteAnyway, the second chart is kind of a neo-Fisherian result, correct (rising interest rates causing higher inflation)? I would argue that this really shows the impact of the the central adopting a new, higher inflation target. They are basically increasing the growth in money supply, all else equal, compared to the steady state. The line with the 0.9 Taylor rule implicitly assumes that the Fed perpetually leaves interest rates below inflation. Of course that will result in a permanent increase in inflation. That's why the original Taylor rule is closer to 1.5.
The important question, however, is if the Fed will continue to keep the 0.9 rule that you suggest. Core PCE inflation is around 5% and the Q4 2002 Survey of Professional Forecasts suggests that it will fall to 2.7% by Q4 2023. The 0.9 Taylor rule would imply that the Fed would be cutting significantly next year, but that's not part of their Summary of Economic Projections (the most recent ones, and likely the ones released tomorrow).
The Fed isn't just setting the short-term yields, but also influencing the whole yield curve based on the market's anticipation of future policy (influenced by forward guidance). Even if short term real yields might be negative (which I'm not really sure about), five-year and longer TIPs yields are positive. If the Fed was following a 0.9 Taylor rule, then how would that be the case?
I struggle with the fiscal models you've been outlining. I don't believe it s for lack of understanding of the underlying mathematics, and I'm hoping that you might be able help me understand why you choose them as a useful parameterization of the world.
ReplyDeleteMy understanding is that from the most simple model, to ones with increasing levels of complexity, the equations admit one of two equilibrium solutions.
First is the unstable equilibrium, where inflation diverges from the current interest rate. Keeping inflation from rolling away to crazy land would require nimble fiscal and monetary policy to over and undershoot inflation just right to keep price stability.
I don't see how this view is justifiable under the weight of the evidence. First, policy makers are not nimble and have operated under a wide variety of economic theories inconsistent with the balancing act. Second, there are large periods of time where inflation increases under higher interest rates and decreases under low interest rates. This view just doesn't seem credible.
The second option is the stable equilibrium, where inflation converges to whatever the interest rate is. This seems, if anything, more far fetched than the unstable equilibrium. Want lower inflation in the long term? Lower the interest rate! This flies in the face of basically all conventional wisdom and experience from Volker to Erdogan to Nabiullina.
You recognize this in previous writings "uncomfortably, long-run neutrality means that higher interest rates eventually produce higher inflation, other things (and fiscal policy in particular) constant." However, I don't feel that the sheer ridiculousness of it has been sufficiently addressed. How is it that every time we look, high interest rates put downward pressure on inflation and low interest rates put upward pressure, when the model implies the opposite? Where is the empirical evidence for convergence?
I'm sure I'm missing something because these tensions are not something you are blind to. I do wonder though whether they imply that that the functional form that you are working with is not the right one in terms of modeling inflation dynamics in the actual economy if the two potential behaviors that they allow are both lacking in credibility.
The key phrases: " So long as fiscal policy doesn't add fuel to the fire....as long as we don't have another fiscal blowout....but without progress on fiscal policy..." Even the Grump may start to realize that all this talk on interest rates is measuring the wrong things --> interest rates. Monetary policy is totally the wrong tool in modulating economic activity/inflation. It's like pushing on a string. Increased interest rates injects money into the private sector - offsetting some of the recessionary effects. It's the monetary policy which should be used. The solution is Job Gty and automatic across the board tax increases (asset value, income, VAT) which kick in when inflation hits certain targets.
ReplyDelete*its the FISCAL policy which should be used....
DeleteI think as long as we can find a second SPR to empty in 2023, inflation will die off.
ReplyDeleteThe annualized monthly inflation as well as the expected future inflation are both likely below current interest rates
ReplyDeleteToo much emphasis is being placed on a version of the new Keynesian DSGE 2-equation model which is subject to very restrictive assumptions. That model is described in an earlier blog posting.
ReplyDeleteThe new Keynesian Phillips Curve, pi(t) = beta•E{pi(t+1)|Q(t)} + kappa•x(t), fails to fit the observed dynamics. Several explanations have been proposed, of which one that asserts that kappa is a state-of-nature-dependent variable instead of a parameter (e.g., a constant) offers better fidelity with empirical observations albeit at the cost of greater mathematical complexity.
The basic 2-equation new Keynesian model can be reduced to demonstrate that raising the interest in the model does diminish the rate of inflation, ceteris paribus, when expectations of pi(t+1) and x(t+1) are held constant.
Setting
In the nK-IS equation, replace the nominal interest rate minus the expected inflation rate with the real rate of interest, r(t). Next substitute for x(t) in the nK-PC equation the right hand side of the nK-IS equation to find
x(t) = - sigma•r(t) + E{x(t+1)|Q(t)}
pi(t) = - sigma•kappa•r(t) + kappa•E{x(t+1)|Q(t)} + beta•E{pi(t+1)|Q(t)}
The state-of-nature inputs to this model are the conditional expectations E{pi(t+1)|Q(t)} and E{x(t+1)|Q(t)}, and the real interest rate, r(t). The outputs are the rate of inflation, pi(t), and the output gap, x(t). The sign on the real rate of interest is negative in both equations, as it should be. The central bank in raising the the nominal rate of interest at a rate exceeding the rate of change in the rate of inflation, narrows the gap and raises the real rate of return removing one source of impetus feeding the rate of inflation even though it may appear that the real rate of interest remains negative.
The key interest rate is not the FED Funds rate, per se, but the U.S. bank prime lending rate which sets the interest rate on borrowed money in the corporate sector for working capital and term loans supporting investment in bolted-down capital (to borrow Karl Shell's terminology).
Setting E{x(t+1)|Q(t)} = x(t), and E{pi(t+1)|Q(t)} = pi(t) gives the long-run values of x(t) and pi(t) in terms of the nominal rate of interest. This is important where the central bank authority has specified a target rate of inflation, say pi*=2%/annum. That long-run, or steady-state, value is i(t)=pi*, as John's charts show, and r(t)=0%, and x(t)=(1 -beta)/kappa > 0.
In this development, I have disregarded the term -sigma•log(beta) for convience.
The important point to stress is the fact the nK-IS and nK-PC curves are are not state transition equations in any sense of that term, but are necessary first order conditions on two distinct and separate optimization problems. Furthermore, the equations are linearity around a long run steady-state that may or may not be trending or stationary. Although not a requirement on the nK-IS equation, it is a requirement on the nK-PC equation and that makes a world of difference, mathematically.
Errata: the last equation in the sentence "That long-run, or steady-state, value is i(t)=pi*, as John's charts show, and r(t)=0%, and x(t)=(1 -beta)/kappa > 0." should read "x(t)=[(1 -beta)/kappa]•pi* > 0"
DeleteThe O/N RRP still has 2 trillion invested, cash for “certificates of confiscation”.
ReplyDeleteLarge CDs signal a recession
ReplyDeleteLarge Time Deposits, All Commercial Banks (LTDACBM027NBOG) | FRED | St. Louis Fed (stlouisfed.org)
Economists just don’t get it. Banks don’t loan deposits. An increase in bank-held savings destroys the velocity of circulation. So, we get FOMC schizophrenia: Do I stop because inflation is too high? Or do I go because R-gDp is falling?
All monetary savings, bank-held savings, originate within the commercial banking system. Demand deposits are just shifted into time deposits.
Since time deposits (income held beyond the income period in which received), a component of M2, originate within the banking system (and there is a one-to-one relationship between time and demand deposits — an increase in TDs depletes DDs by an equivalent amount), there cannot be an “inflow” of time/savings deposits and the growth of time/savings deposits cannot, per se, increase the size of the banking system.
From a system standpoint, TDs constitute an alteration of bank liabilities, their growth does not per se add to the “footings” of the consolidated balance sheet for the system.
John, how do you think Summers’s research on CPI being incorrectly measured fits into the history of the 1970s inflation (e.g, fed funds minus correctly measured inflation was bigger). How do you think the disparity of expectations fits into dynamics today? Last NY Fed survey shows 20% of the population expects deflation in the next year but the 75th percentile expects 9% inflation
ReplyDeleteI haven't followed inflation measurement closely enough. I should. My impression is that measurement makes a big difference over long horizons -- are people better off than in the 1970s (especially in different demographic categories) -- but not much in the shorter run. However, just looking under the hood leads one to worry. Is housing the price or the "rental equivalent?" With more of the economy run by the government, what's the deflator for that? I hope the recent surge leads to more interest in these questions, and somehow I find the time to look into it more. Your second question is really interesting. Lots of research on survey expectations, mostly looking at the average. OK, the average survey expectation is somewhat revealing and somewhat nutty. But what do we make of the huge variation across people in how they answers surveys about anything, from inflation to stock market to the return of Elvis?
DeleteYou can apply Shadow Stats measure of inflation or apply today's measure to yesteryears. It doesn't matter. It's not a Blinder says:
DeleteAlan Blinder says that “food shocks and OPEC ii (supply shocks) deserve much more blame for the alarming rise in inflation in 1979-1980.” No, long-term money flows are down this Nov. and Dec.
John, thanks for the reply! Carola Binder has pushed the envelope a bit on expectations uncertainty, but practical expectations seem wildly understudied, and market indicators of inflation expectations are of course infamously illiquid and limited. You make a great point that uncertainty about the stock market befuddles observers as well, but at least we have a very liquid options market which allows for hedging and some insight.
DeleteFrom the Fed's last SCE, one year ahead uncertainty (expressed as an interquartile range of a smoothed density forecast) has eased but remains at 4%! Such high uncertainty seems inflationary itself, in the same way that stock market uncertainty (e.g., VIX > 30) is correlated with investors selling stocks. In a world with 5% interest rates, even if you expect inflation to be 4%, but you think there's a 25% chance that inflation will be 6%, you would probably still be axed to buy real assets and sell cash. And I'm putting aside the 25% of the population, whom with 9% expectations still experience real rates as deeply negative, but who still have high uncertainty themselves. I would love to ask Allan Meltzer for a quip right about here.
*Apologies for the anonymous posting. I'm a former undergrad student at Stanford, but now in the real world with an employer who wouldn't want me posting about macro, even out of academic interest. I miss the Hoover/Stanford community and tutelage. Merry Christmas!
There have been discussions about whether or not the Fed should raise its inflation target. From this model's implications---a higher inflation rate in the future, would you expect the Fed will increase its inflation target rate, perhaps to 3%?
ReplyDeleteCorrecting the housing component measure within the Consumer Price Index, All Urban Consumers, has a modest effect on CPI-U inflation rate pre-1983. It lowers the peak inflation rate for 1980-81 from about 15% per annum to about 11% per annum. Correcting the housing component measure and applying the 2022 price index component weights reduces the peak rate of inflation circa 1951-52 from about 9.5% per annum to about 5% per annum, and the peak rate of inflation circa 1975 from about 12% per annum to about 9% per annum. But, applying the 2022 price index weights to prior periods is a chump's game--the weights in each period reflect hedonic adjustments that purportedly reflect the cost of the component after adjusting for differences in the utility delivered by consumption of the component (e.g., IBM-PC compatible computers in 1981 had fewer capabilities than IBM-PC compatible computers in 2022).
ReplyDeleteThe OER adjustments are justifiable. Applying the 2022 component weightings to 1981-82 price indexes are not.
The paper presents several charts that are worth viewing. The key take-away is that economic sectors which are exposed to foreign competition (i.e., imports) have seen their importance in the CPI-U index diminished over time, while those sectors of the economy which are insulated from foreign import competition have generally seen their importance increased over time. E.g., articles of women's and girl's clothing have diminished importance; medical services have increased importance. Owner's equivalent rent (OER) importance has largely remained static.
Reference: "Comparing Past and Present Inflation", Bolhuis, M. A., J. N. L. Cramer, L. H. Summers. Cambridge, MA 02138, June 2022, Working Paper 30116. http://www.nber.org/papers/w30116.
All measures of the rate of inflation are estimates only; none purport to measure the true rate of inflation, but claim to be unbiased estimators. The Bolhuis, et al., working paper raises doubts as to the claim of unbiased estimators.
Does it impugn the theoretical Euler equations? Not at all. Theory is not concerned with measurement errors in the price indexes, whether those be of the price level or the output gap. In physics, the parallel is the Navier-Stokes equation of motion of viscous Newtonian fluids (e.g., water, air, oil, etc.) The Navier-Stokes equation cannot be solved for turbulent flow of a viscous Newtonian fluid; it can be approximated numerically, to a reasonable degree of accuracy, given a suitably capable computer system. That is one reason why climate-change models have limited predictive ability.
In a practical sense, in macroeconomics, the central banks are each solving a model when they purport to be tackling the scourge of 'inflation'. Which measure of inflation are they tackling? Core-PCE inflation, core-CPI-U inflation, CPI-median, CPI-trim, etc.? Which measure of inflation was the FOMC referring to in its policy statement of August 2020, when it claimed that "inflation" was too low for too long? Which measure of inflation does J. Powell refer to in his public statements in 2022? Obfuscation allows the central bank presidents and governors to fudge the numbers and avoid taking responsibility for the negative externalities that their policy decisions generate.
There's nothing new under the Sun.
Yeah, same thing for the Fisher equation, which interest rate?
Delete"...which interest rate?" Excellent question. The FFR tends to used by economists because that is the interest rate manipulated by the FOMC-FRBNY open market operations. The U.S. Bank Prime Rate is the rate that commercial money-banks use as a baseline for their loan interest rates to firms. In recent decades, the USBPR = supra{FFR} + 300 b.p. invariably. The current period value of supra{FFR} = 4.5%/a. yielding USBPR = 7.5%/a. For consumers, the mortgage interest rate is more relevant when housing options change decisions are considered; but for employment, the USBPR is the key rate insofar as it bears on working capital financing decisions esp. in the SME sectors. Today, in the quarter ahead period, if FFR is chosen, then the real rate is negative; if USBPR is selected, then the real rate is positive. J. G. Knut Wicksell (dec.) would have chosen the USBPR as the interest rate to use, over the FFR, as the closest analogue to his concept of the natural rate of interest.
Delete