Last Saturday I got to go to the biannual meeting of the Macro-Finance Society. This is a great new effort spearheaded by outstanding young macro-finance researchers.
(The society is limited to people with PhDs after 1990, occasioning the title of this post, a reference to a song about a bar limited to people under 21, a reference you will not get unless your PhD was granted well before 1990.)
I can't blog all the great papers and discussions, so I'll pick one of particular interest, Itamar Drechsler, Alexi Savov, and Philipp Schnabl's "Model of Monetary Policy and Risk Premia"
This paper addresses a very important issue. The policy and commentary community keeps saying that the Federal Reserve has a big effect on risk premiums by its control of short-term rates. Low interest rates are said to spark a "reach for yield," and encourage investors, and too big to fail banks especially, to take on unwise risks. This story has become a central argument for hawkishness at the moment. The causal channel is just stated as fact. But one should not accept an argument just because one likes the policy result.
Nice story. Except there is about zero economic logic to it. The level of nominal interest rates and the risk premium are two totally different phenomena. Borrowing at 5% and making a risky investment at 8%, or borrowing at 1% and making a risky investment at 4% is exactly the same risk-reward tradeoff.
In equations, consider the basic first order condition for investment,
\[ 0 = E \left[ \left( \frac{C_{t+1}}{C_t} \right)^{-\gamma} (R_{t+1}-R^f_t) \right] \]
\[ 1 = E \left[ \beta \left( \frac{C_{t+1}}{C_t} \right)^{-\gamma} \right] R_t^f \]
Risk aversion \(\gamma\) controls the risk premium in the first equation, and impatience \(\beta\) controls the risk free rate in the second equation. The level of risk free rates has nothing to do with the risk premium.
Yes, higher risk aversion or consumption volatility would increase precautionary saving and lower interest rates in the second equation, holding \(\beta\) fixed. But that is the "wrong" sign -- lower interest rates are associated with higher, not lower, risk premiums.
Worse, that "wrong" sign is what we see in the data. Risk premiums are high in the early part of recessions, when interest rates are low. Risk premiums are low in booms, when interest rates are high. OK, I'm a bit defensive because "by force of habit" with John Campbell was all about producing that correlation. But that is the pattern in the data. I made a graph above of the Federal Funds rate (blue) and the spread between BAA bonds and treasuries (green, right scale). You can see the risk premium higher just when rates fall at the early stage of every recession, and premiums low at the peaks of the booms, when rates are at their peaks.
So, if one has this belief about Fed policy, there must be some other effect driving a big negative correlation between risk premiums and rates, yet the Fed can cause premiums to go up or down a bit more by raising or lowering rates.
Every time I ask people -- policy types, central bankers, Fed staff, financial journalists -- about this widely held belief, I get basically psychological and institutional rather than economic answers. Fund managers, insurance companies, pension funds, endowments, have fixed nominal rate of return targets. People have nominal illusions and don't think 8% with 1% short rates is a lot better than 10% with 9% short rates. Maybe. But basing monetary policy on the notion that all investors are total morons seems dicey. For one thing, the minute the Fed starts to exploit rules of thumb, smart investors change the rules of thumb. Segmented markets and institutional constraints are written in sand, not stone, and persist only as long as they are not too costly.
OK, enter Drechsler, Savov, and Schnabl. They have a real, economic model of the phenomenon. That's great. We may disagree, but the only way to understand this issue is to write down a model, not to tell stories.
The model is long and hard, and I won't pretend I have it all right. I think I digest it down to one basic point. Banks had (past tense) to hold non-interest-bearing reserves against deposits. This is a source of nominal illusion. If banks have to hold some non-interest bearing cash for every investment they make, then the effective cost of funds is higher when the nominal rate is higher. We are, in effect, mismeasuring \(R^f\) in my equation.
This makes a lot of sense. Except... Before 2007 non-interest-bearing reserves were really tiny, $50 billion dollars out of $9 trillion of bank credit. Quantitatively, the induced nominal illusion is small. Also, while it's fun to write models in which all funds must channel through intermediaries, there are lots of ways that money goes directly from savers to borrowers, like mortgage-backed securities, without paying the reserve tax. Banks aren't allowed to hold equities, so this channel can't work at all for the idea that low rates fuel stock "bubbles."
And now, reserves will pay interest.
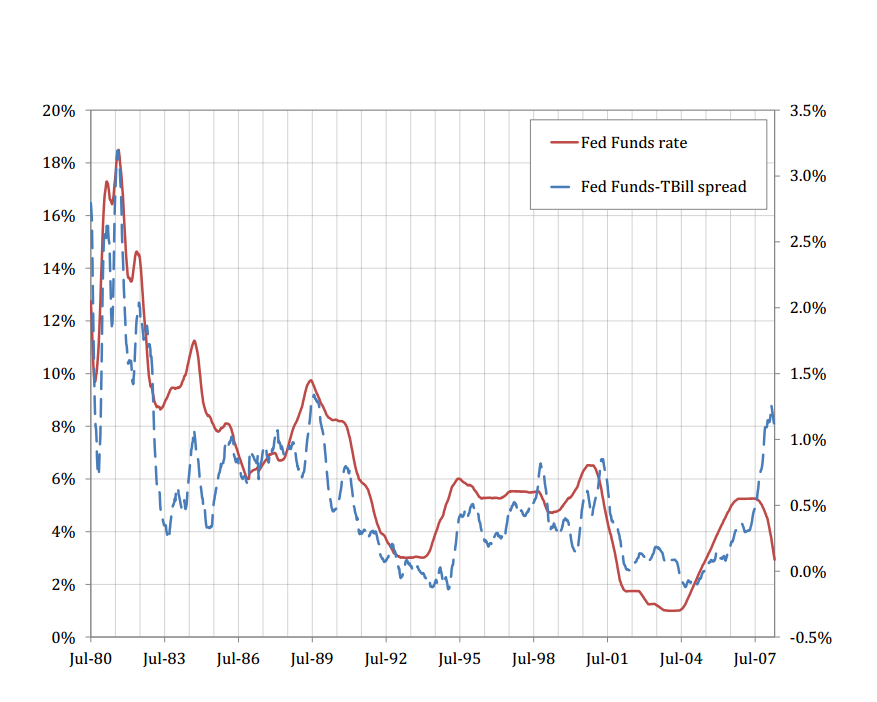
At the conference, Alexi disagreed with this interpretation. He showed the following graph:
Fed funds are typically higher than T bills, and the spread is higher when interest rates are higher. They interpret this quantity (p.3) as the "external finance spread." Fed funds represent a potential use of funds, and the shadow value of lending. Alexi cited another mechanism too: "sticky" deposits generate a relationsip (at least temporary) between interest rate levels and real bank funding costs. So by whatever mechanism, they say, you can see that cost of funds vary with the level of interest rates. In response to my sort of graph, yes, lots of other things push risk premiums around generating the negative correlation, but allowing the causal effect.
Read the paper for more. I have come to praise it not to criticize it. Real, solid, quantiative economic models are just what we need to have a serious discussion. This is a really important and unsolved question, which I will close by restating:
Does monetary policy, by controlling the level of short term rates, substantially affect risk premiums? If so, how?
Of course, maybe the answer is "it doesn't."

I think there is a typo in the 2nd equation. Shouldn't R_{t+1} be inside the expectation? In which case we have the familiar 1=E[M R].
ReplyDeleteI think it should be R^f_t outside the bracket
DeleteYes. Will fix ASAP . Thanks
Delete"Does monetary policy, by controlling the level of short term rates, substantially affect risk premiums? If so, how?"
ReplyDeleteNo, but monetary policy by controlling the rate of change in the short term rates can substantially affect risk premiums.
Supposed you are a leveraged buyer of a 30 year bond with a 6% annual rate of return. Suppose you buy the bond using borrowed money at a short rate of 1%. You roll over that short term debt and the central bank starts raising your cost of financing.
Depending on how quickly the fed raises the short term rate up from 1% will determine whether that will be a profitable investment over its time horizon.
Also, it is unclear from the first graph what maturity of BAA corporate bonds is being used. Obviously, when discerning a risk premium, you need to compare bonds having a similar term to maturity - otherwise you are looking at a mix of term premium and risk premium.
Found it:
Deletehttp://credittrends.moodys.com/chartroom.asp?c=3
The corporate BAA rate used in John's graph is for securities with a term to maturity of 20 years or longer. The spread that you are seeing is part term premium and part risk premium.
http://research.stlouisfed.org/fred2/series/BAA
http://research.stlouisfed.org/fred2/series/DGS30
Combine these two graphs to come up with a rough 30 year risk premium. What you should notice is that 30 year risk premiums rose significantly in two periods - 1978-1982 and 2007-2008.
30 year treasury bonds were introduced in 1977, discontinued in 2002, and re-continued in 2007. And so there is a fiscal element to the risk premium - how can there not be. Shortly after 30 year bonds were introduced / re-introduced, risk premiums rose sharply.
Yeah, I was trying to find some long time series on credit spread purged of term spread, and Baa-10 year has some term. So does Fed funds - T bill. Better measures welcome.
Delete"The level of nominal interest rates and the risk premium are two totally different phenomena. Borrowing at 5% and making a risky investment at 8%, or borrowing at 1% and making a risky investment at 4% is exactly the same risk-reward tradeoff. "
ReplyDeleteINCORRECT. When you borrow at a 5% short rate and make a risky investment at 8%, you have a chance of seeing the short rate reduced from 5% to less than 1% - your nominal interest rate spread has a higher upside.
Also, under which scenario do you realize a higher nominal profit?
Delete1. Short rate starts at 5%, long rate starts at 8%. Short rate rises to 6 1/2%, long rate falls to 6 1/2%.
2. Short rate starts at 1%, long rate starts at 4%. Short rate rises to 2 1/2%, long rate falls to 2 1/2%.
Your capital gain from 8% long interest rate to 6 1/2% long interest rate is 8/6.5 - 1 = 23%. Your capital gain from 4% long interest rate to 2 1/2% long interest rate is 4/2.5 - 1 = 60%.
I'm going to venture into this discussion, even though it is a bit technical and I am somewhat lacking in credentials. But can we consider the effect of missing markets? Let's say I want a return of g from my liquid assets, but there is no asset on the market that pays exactly that. I need to synthesize a return of g using stocks and bonds. How do I maintain my position after a shift in monetary policy? If the risk-free rate is lowered, I bid up the price of stocks, raising the risk premium. I don't have a problem with your Euler equations, but am trying to suggest the effect of frictions.
ReplyDeleteThis is a repeat of the agency problem pointed out at the top. What you describe is a behavioural mirage, and not a structural parameter.
DeleteI would like to see a post on the paper John Cochrane presented at Stanford, the one in which the virtues of a large Fed balance sheet are extolled. I read the paper online. However, I took calculus at Berkeley, and I even passed, but that was almost 40 years ago not sure I can wend my way through your paper. A dumbed down version would be appreciated.
ReplyDeleteHow about credit risk premiums and Fed policy are determined by the same thing, namely the state of the economy. Generally the Fed cuts interest rates when the economy is sick. When the economy is sick, so are firms. Credit risk should be high. After a while, the Fed gets ahead of the curve and policy is easy. Economy gets better. Firms get better. Credit risk goes down. I guess this is a story and I have no idea how to put it in fancy equations, but it would seem more parsimonious than inventing things that don't exist (reserve requirements) just to build out a fancy model, but hey, you got to pay the bills somehow, right? You might want to build in some endogenous beauty contest into the whole investment cycle thing too. Gonna be hard to model, but that's the thing, people aren't equations and fortunately markets aren't either.
ReplyDeleteYou are describing processes of adjustment, while Prof. Cochrane's equations attempt to describe the equilibrium that results, and how it is determined by parameters beta and gamma. But he is willing to look at more complex models, such as those proposed by the Macro-Finance Society. I wonder what he thinks of the "Money View" advanced by Perry Mehrling, especially since we are talking about the effect of central bank actions. Mehrling got his Ph.D. before 1990, which makes him ineligible for the Macro-Finance Society, but we should also be attentive to people with seasoned perspectives!
ReplyDeleteI've always thought that reduced nominal returns (and hence reach for yield) should only matter for entities with zero cost of funds - i.e. investors whose funds are not borrowed. Reach for yield is likely when the entity has 'fixed' liabilities, especially if they are nominal or sticky. In order to meet the liabilities the entity needs a minimum nominal yield. Since cost of funds is zero, only the nominal yield matters. If nominal yield drops below the liabilities, then the entity will 'reach for yield'.
ReplyDeleteIn English that means retiree's living on savings (which is nominal yield and not a spread) have monthly bills to meet. If the savings yield drops far enough, they either reach for yield or fail to pay the rent. Which do we suspect they will do?
Banks on the other hand borrow their funds. The earnings for a bank is the net-interest-margin (go read a 10-K for evidence; the key figure is not nominal rate, the key figure is always NIM). For a bank the yield needed is some minimum spread. Of course if spreads compressed at ZLB -- revenue yield dropping more than cost of funds -- there could be an issue.
"OK, I'm a bit defensive because "by force of habit" with John Cambpell was all about producing that correlation."
ReplyDeleteOK, maybe I'm a bit biased because of Joseph, but shouldn't that be "Campbell"?
Someday I'll learn to type. Thanks.
DeleteYou're welcome! (Glad I haven't lost my typo-spotting touch!)
DeleteIf its "Sugar Mountain" by Neil Young, I know it very well from the Live Rust movie of the 1980's ... and I got my PhD in 1993.
ReplyDeleteReally enjoyed this post, but dumb question about "Yes, higher risk aversion or consumption volatility would increase precautionary saving and lower interest rates in the second equation, holding β fixed."
ReplyDeleteDoesn't a larger gamma/risk-aversion increase the risk-free rate?